Languages and Machines

I think one of the most interesting aspects of theoretical computer science is its exploration of the relationship between machines and languages. If we're trying to understand what it is possible for computers to compute, one way to define computability is in terms of the languages computers can understand (or 'recognize' in the jargon). There are many models of computers, but three have become canonical. What is particularly interesting is that these models can be defined in two ways: either in terms of their functionality or by the languages they can recognize. Machine and language are two sides of the same coin.

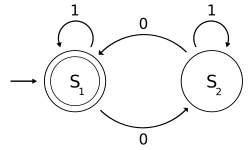
The first, and simplest, model of a computer is a state machine. A state machine has a finite set of states and inputs it can receive. It has a start state and at least one final state. Its next state depends on its current state and the input it receives. The language it accepts is the set of inputs that leads to a final state. For example, the machine to the right accepts the inputs ∅, 1, 00, 0101, and an infinite number of other inputs. All these inputs together define its language.

All state machine languages have a similar form. They're called regular languages and are often used to pattern match a set of inputs, which are defined by regular expressions. For example, the regular expression (0 + (1(01*0)*1)* defines the language of all binary numbers divisible by three. Regular expressions are useful for find-and-replace-like operations, or for tokenizing text. Regular languages are the simplest possible language, since they are characterized by repeating a set of inputs.

The second class of machines are stack machines. A stack machine doesn't just store the current state; it also contains a stack of states that, along with the input provided, determines the next state. Otherwise, it's pretty similar to a state machine. This extra bit of space, though, lets stack machines recognize languages that state machines can't recognize. For example, while state machines can handle L(a*b*), or the set of strings having any number of a's and a's, they can't handle {aⁿbⁿ}, or the set of strings in which a's are followed by an equal number of b's.

Stack machines recognize recursive or context-free languages, which are more powerful than regular languages. The context free grammar for the language {aⁿbⁿ} is S -> aSb | e, where e is the empty string. Each S can be replaced with either aSb or the empty string. It is 'context free' because you can only replace an S with aSb when you already have an S there. Context free languages are surprisingly powerful. The rules governing formal sentence creation in almost all human languages can be expressed with a context free grammar. A sentence S can be replaced with a noun phrase (NP) and a verb phrase (VP), which can in turn be replaced with other particles of speech.

Finally, the third class of machines is the Turing machine. Unlike stack machines, Turing machines have a head which can read and write to a tape and can move in either direction. With this simple addition, we have the most powerful computer in the world. No more powerful model has been found. Turing machines can execute algorithms. They can recognize {aⁿbⁿcⁿ}, as well as {a*b*} and {aⁿbⁿ}.

In fact, Turing machines are so powerful that they can run programs that are contradictory or that lead to infinite loops. Since Turing machines can understand complex languages, and since any language of sufficient complexity can have contradictory statements (such as 'This statement is false'), it's quite possible to feed computers inputs that make no sense. The classic demonstration of this is the Halting Problem. If it were possible to write a program that could tell you if another program got stuck in an infinite loop or completed, you could write an inverse of that program that went into an infinite loop if the program fed to it completed and completed if it never stopped. Feed this program to itself and you have a program that stops when it doesn't and doesn't stop when it does. Contradiction!

I've always found this argument a little sterile, but I think the important thing is that some things are uncomputable even if we're able to express them in code. These problems are 'recursively enumerable' but don't qualify as recursive languages, in which all inputs can be computed on any Turing machine. Recursively enumerable languages are semi-decidable, meaning that some inputs may complete but others will not.

Interestingly, while no more powerful computer than the Turing machine has been discovered, there is a fifth and final class of language outside the other four classes and which cannot be computed at all. These are a little hard to grasp, but the complement of a language that halts provides an example. In this language, a computer would run forever and then accept, which is obviously impossible.

Theoretical computer scientists like automata and formal languages because they can be studied with mathematical rigor. I'm not so interested in this. Instead, the connection between languages and machines makes me wonder about the kinds of languages that humans can understand. What kind of machines are we? Are there other languages out there we can't understand? What makes them languages? Are there computers that can understand languages that we can't? Are there more powerful machines than Turing Machines? Do we have the ability to invent them?

What Time is it?

From this deduction of our faculty of cognizing a priori there emerges a very strange result, namely that with this faculty we can never get beyond the boundaries of possible experience, that such cognition reaches appearances only, leaving the thing-in-itself as something actual for itself but uncognized by us. -- Imannuel Kant, The Critique of Pure Reason

The question of whether a computer can think is no more interesting than the question of whether a submarine can swim. -- Edsger Dijkstra, The Threats to Computing Science

In the late 1700's, Kant decided to demonstrate the limits of thought. This is not so easy, because we can think of all sorts of things that are impossible, like flying horses or projects that ship on time. Furthermore, the only tools we have are our pitiful human brains. The only way we can undertake to critique--i.e., set bounds to--pure reason is by reason itself. Kant's conclusion is that our understanding is limited by the structure of human experience. We can't be sure of grasping things as they truly are.

Which metaphysics is right is still up for debate, but we have made major inroads in the somewhat related field of computability. Of course, things are a bit easier here, since we're the ones who thought up the idea of computers, and they do what we tell them to do (for the most part). However, the idea is roughly parallel. Theoretical computer science is to computers what metaphysics is to thinking. Kant's question was: What is it possible to know? The question facing theoretical computer science is: What is it possible to compute? Since computers cannot think, as Dijkstra reminds us, we should be content with this more reasonable question.

In a later post, I'll talk about computation from the side of computability, which involves lots of serious proofs to determine what is logically possible for machines to do. Here, I'll discuss complexity theory, which asks: What is within the computational ability of actual computers, considering the real limitations of time and space?

One of the basic problems of computing is figuring out how much time it takes for a computer to solve a problem. As Donald Knuth found, it all depends on your problem and the algorithms you have available to solve it. Some problems take a polynomial (P) amount of time to be solved, which means that, as the input size increases, the amount of operations needed to solve the problem increases on the order of xⁿ, where n is an integer. If you have a list of 100 items, and your algorithm is on the order of x², it will take around 10,000 operations.

Some algorithms, however, grow with non-polynomial (NP) or exponential time as input size increases. They're on the order of n^x, where n is an integer. With small input sizes, this is not so bad. But with an input size of only 100 on an O(2^x) problem, you're looking at around 1,267,650,600,228,229,401,496,703,205,376 or > 1.3 * 10³⁰ operations. That is a lot. If you can do 10 trillion operations per second, that will still take far longer than the lifetime of the universe to finish--about 100 quintillion years.

NP problems are not esoteric. They're often graph problems, liking trying to determine the shortest distance someone can travel in order to visit a bunch of places without visiting the same one twice (the travelling salesman problem). Any problem involving scheduling or fitting items into boxes is NP too. I've often wondered how the modern world of logistics is possible, considering all of its problems are NP!

Theoretical computer scientists have shown that some problems are NP-complete, meaning that other NP problems can be reduced to them. They're the hardest possible problems to solve in NP time. The first problem shown to be NP-complete is Boolean satisfiability (or SAT), which involves determining the values of variables in a Boolean expression such that it evaluates to true. Since NP problems are so important and so intractable, many people have hoped to find a way to solve an NP-complete problem in polynomial time. If this happened, all NP problems would suddenly become tractable.

I'm not holding my breath for anyone to show that P=NP or to invent a non-deterministic computer, which would branch its computation at every decision and run NP problems in P time. So, what can you do?

Years of research have come up with a few ideas. If your run-time is NP, you can do a lot of preprocessing, as long as it takes polynomial time. You may be able to eliminate a lot of obviously wrong choices, or you may be able to figure out certain elements of a solution. For example, if your boolean satisfiability problem has a term by itself, it must be true. With preprocessing, you can get performance down to O(1.4^x) or so on some problems.

Another option is to find a slightly easier problem. If you don't care about obtaining the best possible solution, you can usually find an algorithm that performs no worse than twice as badly as the ideal. For example, greedy algorithms tend to do pretty well on graph problems, though there are pathological cases. For many applications, it's better to have a reasonably good answer than none at all.

To be honest, though, I've never run into a problem at work where I even had to consider NP solutions. Perhaps I have been lucky (or perhaps it's because I don't work in logistics!). It's worth wondering how important it is to know about the issues facing NP algorithms. For one thing O(1.1^x) is better than O(x¹⁰). Furthermore, there are problems that are even harder than exponential problems, such as finding a winning move in chess. Each move has a tree of exponential solutions to investigate.

I think the important thing to understand is that certain problems get really hard to solve really fast. Computers follow instructions, and if the only possible instructions require looking at a huge number of possible solutions, it's going to take a long time. Humans process a lot of information very quickly because we filter out much more than we pay attention to. Until computers become better pattern-matchers, they won't be able to match our speed in processing large input sizes. This is why there is so much interest around machine learning now, though programming computers to be better pattern-matchers will have its own problems, since heuristics always fail for outliers (see Kahneman's Thinking, Fast and Slow).

Most theoretical computer scientists do not think P=NP. This is probably a good thing--at least for the time being. Cryptography, for example, would cease to be possible if prime factorization algorithms could be solved in polynomial time. You remember Sneakers, right? Anyway, I think it's more interesting to try to make computers smarter than to try to make them faster at doing stupid things. In other words, we shouldn't hope to get computers to grasp the thing-in-itself through further and further analysis; we should seek to change the structure of their 'experience.'

Waste Not

One of the last projects in my dad's long career was in biomedical manufacturing.  It took five years and never went to market.  In that time, his team learned a number of things, particularly about the production of ceramic seals having certain tolerances.  The difficulty in doing this with sufficient quality ultimately stymied the project.  I remember asking him what would happen to all of the knowledge the team had acquired.  Would they share it with the manufacturing community?  How could it be ensured that others could learn from their experience?

Learning is at the heart of the Lean Startup movement, which takes its inspiration from the short cycle times of small batch Lean manufacturing processes.  Eric Ries wrote down the principles of the organizational processes that many successful startups have used.  Many startups find that their original idea goes through many iterations before becoming a successful product.  The worst thing a startup can do is spend a year 'perfecting' a product no one wants.  So, startups should get an (imperfect) product out there, see how people use it via actionable metrics, and modify it and their assumptions accordingly.

The Lean philosophy is essentially about embedding the scientific method into product development processes.  Since you can't rely on customer feedback to learn how people use or could use a product, you should build reporting into your software from the start, not as an afterthought.  Your software should also be able to run A/B tests where some users are given a new interface while a control group sticks with the old one.  The ways in which customers will use a product should be tested by its use.

In a certain way, this is all very straightforward.  No one wants to think that they are not thinking scientifically when evaluating a product, but being Lean is hard.  The scientific method has to be at the heart of everything you do.  It touches what is built as much as how it is built.  The product development and product planning teams have to work very closely together.  Developers can't just build whatever product people think up.  I know of many organizations that could not work this way.

Though Ries's advice is sound for software startups, his main target is waste at a societal level.  Think of all the billions of dollars and hours of time wasted pursuing products that were not or could not be rigorously hypothesized, tested, or proven due to imperfect processes.  The problems of product development are people problems, not technological problems.  Ries shows how to cut waste at an organizational level, with benefits that will be felt throughout society as people start to adopt the principles.

Still, Lean doesn't really help with the problem facing my dad's organization.  What techniques or technologies can be used to share information between organizations?  This may not be a general problem that can be solved.  And, after all, if companies share everything about what they've learned, what advantage do they have in the marketplace?  By writing down Lean principles, Ries is helping to share best practices about management, but there are plenty of domain-specific problems and best practices out there to be tackled.

Information and Identity

We like to think of ourselves as somehow apart from all this information.  We are real — the information is merely about us.  But what is it that is real?  What would be left of you if someone took away all your numbers, cards, accounts, dossiers and other informational prostheses?  Information is not just about you — it also constitutes who you are.  -- Colin Koopman

In the last 100 years, many philosophers have explored the ways in which identity is shaped by cultural norms, concepts, and practices.  Michel Foucault is famous for having shown how very basic ideas, like sexuality and sanity, have changed over time as cultures have changed.  Concepts like 'sane' or 'straight' empower some at the expense of others, but there is no man behind the curtain forcing us to think about ourselves in a certain way.  We do it to ourselves.  For example, we police ourselves when we have thoughts that are 'crazy' or 'deviant,' and we treat others according to how they match up to our expectations, for instance by shunning or even institutionalizing them.

Colin Koopman, an old colleauge of mine, recently published a great piece in the Times' Stone series.  Too much technology writing is either breathlessly optimistic (this new technology will save the world!) or pessimistically tears apart the weak arguments of the optimists (never a hard thing to do).  Koopman's approach is different.  When discussing the value of technologies, he says, we need to consider how they impact our identities.

In some ways, this idea is obvious.  Information technologies, after all, are about information, and you can't understand yourself or anyone else without information.  But few people are actually talking about this.  For example, self-monitoring technologies are changing how we think about ourselves.  People are quantizing, sharing, and comparing their fitness activity, their sleep, and their (supposed) mental acuity.  What kinds of values do these technologies embody?  Do they help us become more moral, just, or honorable?  Do they make us better friends or family members?  The things we spend our time doing shape who we are, and taking the time to do one thing means we don't have time for something else.

Koopman is particularly interested in the information technologies associated with governments, which are used to monitor and control us.  When you know that your phone calls are being surveilled and that a record is being kept on you, you act in a certain manner.  If you don't, you may not be able to get a job, or you may even be detained indefinitely.  A hundred years ago, you could leave town if you got into trouble, but now your record travels with you wherever you go.  'Identity theft' means that someone has gained access to private data, not that they have stolen someone's personality or personhood.

Since philosophers can't provide solutions, Koopman doesn't offer one.  The philosopher's job is to help us think better about problems.  As a society, we need to decide what kinds of information should exist, what kind of monitoring is legal, and what kinds of categories should be used to define us.  Technology writers should stop praising or condemning technologies in general and should us talk about what kinds of technologies we actually want.  And we all need to think about what kinds of people specific technologies make us, and whether or not those are the kinds of people we want to be.

Two Ideas

In the 1930’s, Claude Shannon had two ideas that gave rise to modern computing.  The first is that logic can be expressed in electrical circuitry.  In 1854, Charles Boole developed a form of logic in which the only possible values are true and false.  The possible operators are ‘and’, ‘or’, and ‘not.’  Before this, the dominant form of logic had been developed by Aristotle.  (All men are mortal.  Socrates is a man.  Therefore, Socrates is mortal.)  Boole’s logic made set theory and statistics possible.

Shannon realized that the presence or absence of a current could notate truth or falsity and that Boolean operators could be implemented using simple circuits.  ‘And’ can be implemented by a series circuit.  ‘Or’ can be implemented by a parallel circuit.  And ‘not’ can be implemented by a relay.  These simple components are the building blocks of today’s more complicated machines.

Shannon’s other idea is a postulate that all information can be expressed in Boolean logic. This postulate defines the field of information theory.  It is now obvious to us that all numbers can be represented using a binary number system and that all symbols can be codified in systems of representation like ASCII, but this was not at all obvious at the beginning.  Many early computers, like the ENIAC, still used a decimal number system, for example.

Here’s a simple example showing these two ideas at work.  A one bit adder can be built using an exclusive or (XOR) gate and an AND gate.  The truth table is:

INPUTS                 OUTPUTS

A             B             SUM      CARRY

0              0              0              0

0              1              1              0

1              0              1              0

1              1              0              1

In logic gates, this can be implemented using the following:

Just stop and think about this.  Using two very simple components we have implemented an adding algorithm.  It even carries the one.  You could chain a few of these together and add numbers as large as you like.  Just rig up some light bulbs, power sources, and switches, and you'll have your I/O.

It’s hard to appreciate now just how much of a conceptual leap Shannon's two ideas were.  I took multiple semesters of computer hardware design and never really got it.  Charles Petzold’s book Code helped.  He shows how simple the technologies at the heart of computing really are.  In fact, they had been around for a hundred years before Shannon’s work reconceptualized the ways those technologies could be used.  Petzold shows how telegraph relays can be used to build a complex adding machine.

I’m fascinated by Shannon and the history of early computing, even if it’s not directly relevant to my work.  Modern programming languages are so far abstracted from physical computers that I doubt if studying electrical engineering can have much benefit to programmers.  If it’s worth studying, it’s as a system of thought, like physics or chemistry.  But it’s also worth considering these two ideas from time to time.  Are there any forms of logic that cannot be captured by computers?  Are the audiophiles right that analog sound is better than digital?  What gets lost in the translation to transistors?

Finally, the birth of computing is simply an interesting moment in intellectual history.  Shannon’s two ideas let us leap over Babbage, whose difference engine was never completed.  Babbage basically has no intellectual inheritance.  Even if the analytical engine “weaves algebraical patterns just as the Jacquard-loom weaves flowers and leaves,” in Ada Lovelace’s words, punch cards were arrived at independently.  The Von Neumann architecture owes nothing to Babbage's design.

Inca vs. Spaniard

Olduvai Stone Chopping Tool, 2M BC

The oldest technology is food production.   A few million years ago, humans chipped their first stone tools used to cut flesh, break bones, strip trees, and peel roots.  The nutrients our ancestors harvested using such tools set off a virtuous cycle of increased brainpower and better tools.  500,000 years ago, we were making handaxes, and, relatively soon, lasting art. 

Food production is at the center of any civilization.  Agriculture provides a surplus of calories which leads to population growth and a division of labor.  Soon after plants and animals were domesticated, humans created the first governments that paid craftsmen to create public art, like the statues of Ramses II.  Government bureaucrats needed a way to keep track of food distribution, which led to the invention of writing.  This same pattern can be seen in Sumer, Egypt, the Indus River valley, the Yellow River valley, Mesoamerica, and Peru--the so-called 'cradles of civilization.'

It seems odd to think of food as a technology, but it's hard to imagine an industrialized America powered by taro or sago, the foods domesticated in Papua New Guinea and that barely provide enough protein to live on.  According to Jared Diamond, our ability (or inability) to domesticate plants and animals throughout the world led to the drastically different rates of technological progress which, in turn, led to Europeans colonizing the world.  I recently spent a couple of weeks in Peru and visited a number of Inca sites, including Machu Picchu.  It was hard to understand how 168 Spaniards could defeat 80,000 Incas when the latter were able to produce incredible fortresses and stonework, like at Saksaywaman.  Why didn't the opposite happen?  Why didn't the Incas sail to Spain and defeat Charles V?

Making corn in the Andes ain't easy.

The short answer is: because corn took a long time to domesticate.  It wasn't until 2,500 BC that corn was domesticated and spread through the Americas.  Scientists still argue about how it was done, since modern corn bears no resemblance to probable progenitors, i.e., teosinte.  In contrast, wheat and barley may have been domesticated as early as 20,000 BC and were pretty much ready for the taking in the Fertile Crescent.  Furthermore, all five large domesticated animals (cows, pigs, sheep, goats, and chickens) come from the Middle East.  Alpacas and llamas were domesticated in Peru, but they don't provide milk and can't be used as beasts of burden.

These differences in food technology gave Eurasia a long head start over the Americas.  They led to technologies like sailing ships and guns, and the close contact of many humans with many animals led to nasty germs like smallpox, which killed far more people than any Spaniards did (80-90% of local populations, by some estimates).  The Incas didn't even have written language (though they had a system of knots called quipu, which could be easily carried by messengers), so they could not read about Cortes's conquest of the Aztecs/Mexica.  They had no reason to assume that a tiny group of Spaniards could or would capture their king (who was a god, after all) and enslave them.

When I think of technology, I tend not to think about food (unless it's GMOs).  Maybe I'm too immersed in computers and code.  Historically, however, food technology has been a major factor--perhaps the biggest one--in how we live our lives.  I wonder if a similar history could be written about clothing or shelter.  In any event, it's important to put new technologies like Web 2.0 into perspective against long-term historical trends.  Is Facebook really the new corn?

Some Peace and Quiet

It's taken some time, but I've shrugged off much of my childhood shyness.  This change came in part from gaining experience--after all, confidence should follow competence--and in part from the fact that the older you get, the less you give a shit about what anyone thinks.  I had started to feel so at ease in social situations that I was beginning to think that I might actually be a closet extrovert, or perhaps an "ambivert."  That was until I took an introversion quiz.  After answering "yes" to every question ("People tell me that I'm a good listener"; "I enjoy solitude"; "I fear change"), there seems to be no doubt about it.

Hi, I'm Zach.  I'm an introvert.

Being introverted shouldn't feel like something you have to confess, but sometimes it does.  I could relate to the stories Susan Cain tells in her book Quiet and her TED talk, in which she felt shunned at camp if she picked up a book rather than socializing all the time.  She argues that our culture has an "extrovert ideal," where playing well with others is more valuable than having good ideas.  This is a problem because 1/3 to 1/2 of all people are introverts.


It's important to distinguish between shyness and introversion.  Shyness is anxiety.  Even extroverts can be shy--apparently Barbara Streisand is a shy extrovert.  Extroverts and introverts mainly differ in how they react to social stimuli.  Introverts tend to prefer deep conversations and then need time alone afterwards.  Extroverts are stimulated by being the center of attention.  This doesn't mean that introverts aren't social; they're just differently social.

How you recharge your batteries is important for how you should structure your work and personal life.  For example, I try to get to work early to have space to think without interruption.  After any highly social event, like company picnics, I reward myself with time to read or write.  Cain says introverts should have "restorative niches," such as jogs, couches, or bathroom stalls.

Cain rightly emphasizes that many leaders are introverts.  She points to Gandhi, Rosa Parks, and Bill Gates, as well as a study showing that extroverts are better at managing passive employees while introverts are better at managing people who are supposed to think for themselves.  Maybe we needed extrovert leaders in a world of salespeople and factory workers, but now, in a knowledge economy, we need introverts who can listen before they act.

Personally, I hope that we'll soon see the end of open office plans and "visionary" executives.  Why should I listen to anyone who isn't ready to listen to me?